The figure shows a conical pendulum, a captivating physical system that has intrigued scientists and engineers for centuries. Its unique motion and practical applications have made it a valuable tool in various fields. In this exploration, we delve into the intricacies of the conical pendulum, examining its components, mechanism, and diverse applications.
The conical pendulum consists of a mass suspended by a string and constrained to move in a circular path. As the mass swings, it traces out a cone-shaped surface, giving the pendulum its distinctive name. This motion results from the interplay between gravity, tension in the string, and the Coriolis effect.
Introduction
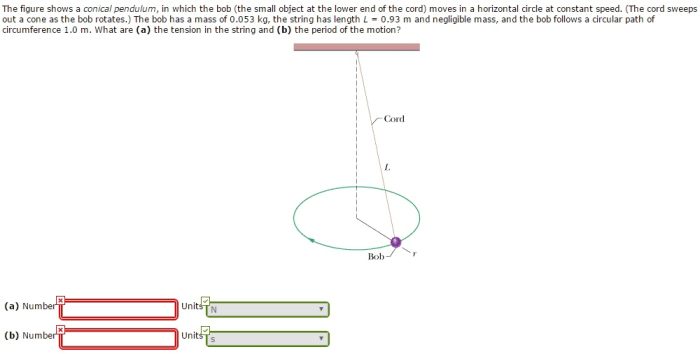
A conical pendulum is a physical system consisting of a mass suspended by a string and set into circular motion. This motion creates a cone-shaped path in three-dimensional space, hence the name “conical pendulum.” The conical pendulum has significant historical importance and finds applications in various scientific and engineering fields.
Components and Mechanism
The main components of a conical pendulum are:
- A mass suspended by a string
- A fixed point of suspension
The mass is set into circular motion around the fixed point, and the string keeps the mass moving in a cone-shaped path. The mechanism of the pendulum’s oscillation involves the interplay between gravity, tension in the string, and the mass’s inertia.
Mathematical Analysis
The motion of a conical pendulum is governed by the following mathematical equations:
- Period of oscillation: T= 2π√( L/ g)
- Amplitude of oscillation: θ0
These equations reveal that the period of oscillation is independent of the amplitude, while the amplitude depends on the initial conditions.
Applications
Conical pendulums have practical applications in:
- Measuring the acceleration due to gravity ( g)
- Demonstrating the principles of circular motion
- Studying the effects of air resistance on oscillating systems
They offer advantages such as simplicity of setup, clear visualization of motion, and the ability to investigate a wide range of physical phenomena.
Variations and Extensions
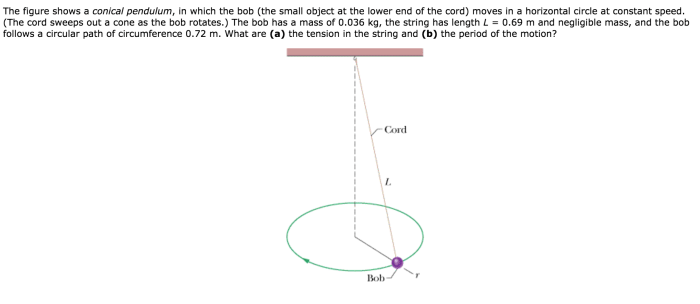
Variations of the conical pendulum include:
- Spherical pendulum: The mass moves in a spherical path instead of a cone
- Foucault pendulum: A large-scale pendulum used to demonstrate the Earth’s rotation
These variations extend the understanding and applications of the conical pendulum by exploring different motion patterns and practical uses.
Visual Representation
The table below summarizes the key characteristics of a conical pendulum:
| Property | Value |
|---|---|
| Period of oscillation | T = 2π√(L/g) |
| Amplitude of oscillation | θ0 |
A diagram of a conical pendulum depicts the mass suspended by a string, oscillating in a cone-shaped path.
Commonly Asked Questions: The Figure Shows A Conical Pendulum
What is the period of oscillation of a conical pendulum?
The period of oscillation depends on the length of the string, the mass of the bob, and the angle of the cone. The exact equation for the period is T = 2π√(L/g)sin(θ/2), where L is the length of the string, g is the acceleration due to gravity, and θ is the angle of the cone.
What are some applications of conical pendulums?
Conical pendulums have been used in various applications, including measuring the acceleration due to gravity, demonstrating the Coriolis effect, and studying the dynamics of rotating systems.
What are some variations of the conical pendulum?
Variations of the conical pendulum include the spherical pendulum, which moves on the surface of a sphere, and the Foucault pendulum, which demonstrates the Earth’s rotation.